디지털 공학 2화 - 펄스, 논리 연산, 게이트

불 대수와 진리표

불 대수와 진리표는 디지털 회로 설계와 논리 회로의 분석에 매우 중요한 도구입니다. 불 대수는 논리 연산을 다루는 대수 시스템이고, 진리표는 논리 연산의 결과를 표로 나타낸 것입니다. 이를 통해 논리 회로의 동작을 명확히 이해하고 설계할 수 있습니다.

​

진리표 (Truth Table)

진리표는 논리 연산의 모든 가능한 입력 값에 대한 출력을 표로 나타낸 것입니다. 진리표는 논리 회로의 동작을 시각적으로 이해하는 데 유용합니다.

​

예시: 두 입력 A와 B의 AND, OR, NOT 연산 진리표

A	B	A AND B	A OR B	NOT A
0	0	0	0	1
0	1	0	1	1
1	0	0	1	0
1	1	1	1	0

불 대수 (Boolean Algebra)

불 대수는 19세기 수학자 조지 불(George Boole)에 의해 개발된 대수 체계로, 논리 연산을 수학적으로 표현합니다. 불 대수는 주로 두 가지 값(참 또는 거짓, 1 또는 0)을 다루며, 기본적인 연산은 AND, OR, NOT입니다.

​

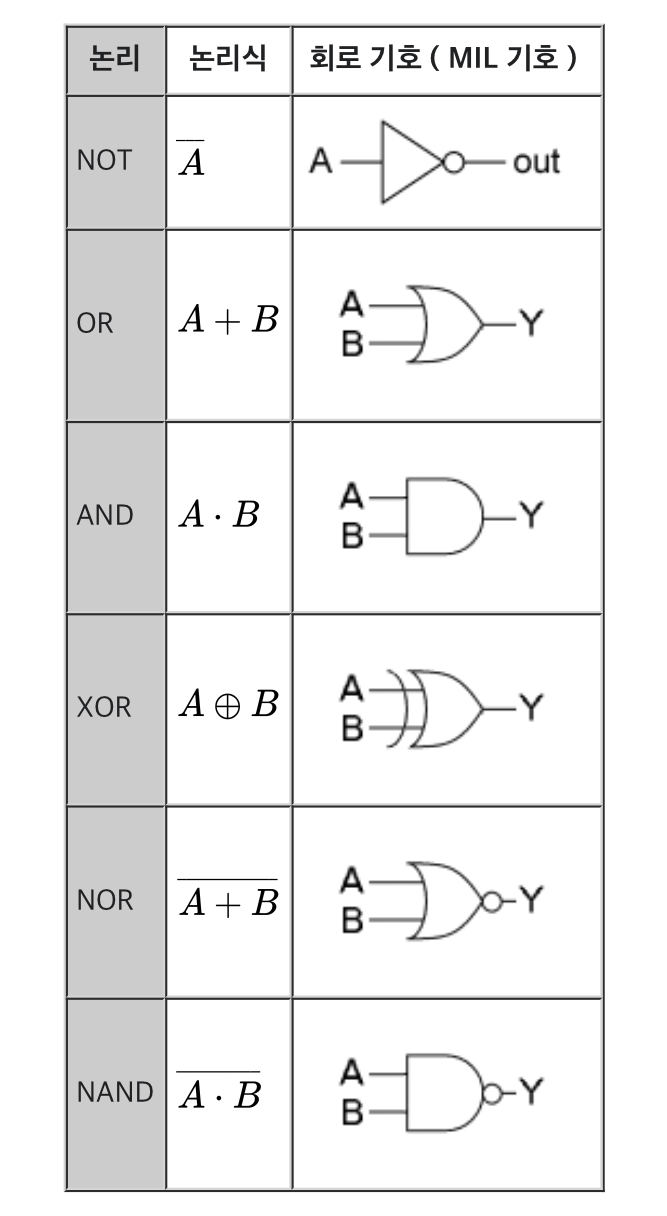
AND, OR, XOR, NOT, NAND, NOR 연산과 게이트

논리 게이트 (Logic Gates)

논리 게이트는 디지털 회로 설계의 기본 구성 요소로, 불 대수 연산을 수행하는 전자 소자입니다.

기본 연산

AND (논리곱)

• 기호: A · B 또는 AB
• 두 입력이 모두 참일 때만 참(1)입니다.
• 진리표

A	B	A AND B
0	0	0
0	1	0
1	0	0
1	1	1

OR (논리합)

• 기호: A + B
• 두 입력 중 하나라도 참이면 참(1)입니다.
• 진리표

A	B	A OR B
0	0	0
0	1	1
1	0	1
1	1	1

NOT (부정)

• 기호: ¬A 또는 A'
• 입력이 참이면 거짓(0), 거짓이면 참(1)입니다.
• 진리표

A	NOT A
0	1
1	0

추가 연산

NAND (논리곱 부정)

• 기호: ¬(A · B)
• AND 연산의 결과를 반전시킵니다.
• 진리표

A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

NOR (논리합 부정)

• 기호: ¬(A + B)
• OR 연산의 결과를 반전시킵니다.
• 진리표

A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

XOR (배타적 논리합)

• 기호: A ⊕ B
• 두 입력이 다를 때 참(1)입니다.
• 진리표

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

XNOR (배타적 논리합 부정)

• 기호: ¬(A ⊕ B) 또는 A ≡ B
• 두 입력이 같을 때 참(1)입니다.
• 진리표

A	B	A XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

펄스 파형과 타이밍 다이어그램

펄스 파형과 타이밍 다이어그램은 디지털 회로의 동작을 분석하고 이해하는 데 중요한 도구입니다. 펄스 파형은 시간에 따른 신호의 변화를 나타내고, 타이밍 다이어그램은 여러 신호 간의 상호 관계를 시각적으로 보여줍니다.

​

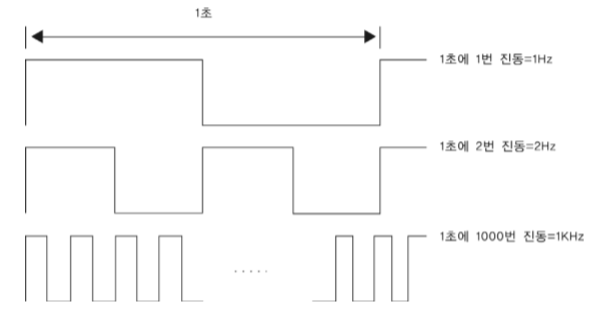
펄스 파형 (Pulse Waveform)

펄스 파형은 디지털 신호가 시간에 따라 변하는 형태를 나타냅니다. 디지털 신호는 주로 두 가지 상태(높음(High), 낮음(Low))를 가지며, 이러한 상태가 시간에 따라 변할 때 펄스 파형으로 표현됩니다.

• 주기 (Period): 하나의 사이클이 완료되는 시간.
• 주파수 (Frequency): 단위 시간당 주기의 반복 횟수. 주파수는 주기의 역수로 표현됩니다 (f = 1/T).
• 펄스 폭 (Pulse Width): 신호가 High 상태를 유지하는 시간.
• 듀티 사이클 (Duty Cycle): 주기 내에서 신호가 High 상태를 유지하는 시간의 비율. (듀티 사이클 = (펄스 폭 / 주기) × 100%)

  

 

타이밍 다이어그램 (Timing Diagram)

타이밍 다이어그램은 여러 디지털 신호의 시간에 따른 변화를 동시에 나타내어, 신호들 간의 관계와 타이밍을 분석하는 데 사용됩니다. 각 신호는 시간축에 따라 변화하며, 특정 시점에서의 신호 상태를 보여줍니다.

구성 요소

• 시간축 (Time Axis): 수평축으로 시간의 흐름을 나타냅니다.
• 신호 라인 (Signal Lines): 수직축으로 각 디지털 신호의 상태를 나타냅니다.
• 상태 전이 (State Transitions): 신호가 High에서 Low로 또는 Low에서 High로 변하는 지점.
• 클럭 신호 (Clock Signal): 주기적인 타이밍 기준을 제공하는 신호.

  

 

펄스 파형과 타이밍 다이어그램은 디지털 시스템의 동작을 이해하고 최적화하는 데 필수적인 도구입니다. 이를 통해 복잡한 회로의 동작을 시각적으로 분석하고 설계할 수 있습니다.

​

부울 표현식을 통한 회로 구현

부울 표현식이 주어졌을 때, 이를 통해 회로를 구현할 수 있습니다.

예를 들어 AB + ~B 를 회로로 나타내면 아래와 같습니다.

 

진리표

A	B	~B	AB	AB + ~B
0	0	1	0	1
0	1	0	0	0
1	0	1	0	1
1	1	0	1	1

조합 논리 회로 (Combinational Logic Circuits)

디지털 시스템에서 논리 회로는 조합 회로(combinational) 이거나 순차(sequential) 회로이다.

논리 회로에서 출력이 현재 입력만의 함수이면 이를 조합 회로라고 한다.

조합 회로는 부울 함수들에 정의된 논리 연산을 수행한다.

이에 반해 순차 회로는 논리 게이트에 저장 회로를 포함한 회로이다.

따라서 순차 회로의 출력은 저장된 값과 입력 값에 따라 변한다.

 

조합 회로 분석

조합 회로는 논리 게이트들의 연결로 이루어집니다.

 

주어진 회로에서 출력의 부울 함수를 구합니다.

 

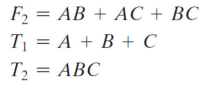
또한 진리표로 표현하여 분석하기도 합니다

 

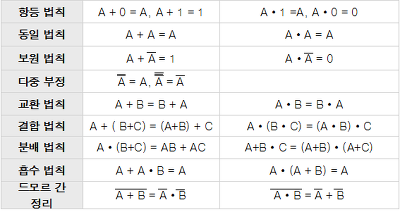
드 모르간 법칙을 포함한 논리 연산 법칙

불 대수 체계에서의 논리 연산에는 일정한 규칙이 있습니다

​

복습 문제

논리식 진리표 작성 문제

1. 논리식: A AND (B OR C)
2. 논리식: (A OR B) AND (NOT C)
3. 논리식: (A XOR B) AND (A OR NOT C)

• 정답

1. 논리식: A AND (B OR C)

A	B	C	B OR C	A AND (B OR C)
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	1	0
1	0	0	0	0
1	0	1	1	1
1	1	0	1	1
1	1	1	1	1

1. 논리식: (A OR B) AND (NOT C)

A	B	C	A OR B	NOT C	(A OR B) AND (NOT C)
0	0	0	0	1	0
0	0	1	0	0	0
0	1	0	1	1	1
0	1	1	1	0	0
1	0	0	1	1	1
1	0	1	1	0	0
1	1	0	1	1	1
1	1	1	1	0	0

1. 논리식: (A XOR B) AND (A OR NOT C)

A	B	C	A XOR B	NOT C	A OR NOT C	(A XOR B) AND (A OR NOT C)
0	0	0	0	1	1	0
0	0	1	0	0	0	0
0	1	0	1	1	1	1
0	1	1	1	0	0	0
1	0	0	1	1	1	1
1	0	1	1	0	1	1
1	1	0	0	1	1	0
1	1	1	0	0	1	0

파형 그래프 작성

1. 논리식: A AND (B OR C)
2. 논리식: (A OR B) AND (NOT C)
3. 논리식: (A XOR B) AND (A OR NOT C)

논리연산 법칙 문제

1. 문제 1: 드 모르간의 법칙을 이용하여 (A AND B)'의 부울 표현식을 간단히 하시오.
2. 문제 2: (A NAND A) NAND (B NAND B)의 부울 표현식을 간단히 하시오.
3. 문제 3: (A AND B) OR (A AND B')의 부울 표현식을 간단히 하시오.
4. 문제 4: (A OR B) AND (A OR B')의 부울 표현식을 간단히 하시오.
5. 문제 5: (A ⊕ B) ⊕ B의 부울 표현식을 간단히 하시오.

• 풀이

1. 풀이 1:

• (A AND B)'는 드 모르간의 법칙에 의해 A' OR B'로 간단히 할 수 있습니다.

1. 풀이 2:

• 진리표 작성을 통해 A OR B 임을 확인 가능합니다.

1. 풀이 3:

• (A AND B) OR (A AND B')는 분배 법칙에 의해 A AND (B OR B')로 간단히 할 수 있습니다.
• B OR B'는 항상 1이므로, 최종 표현식은 A입니다.

1. 풀이 4:

• (A OR B) AND (A OR B')는 분배 법칙에 의해 A OR (B AND B')로 간단히 할 수 있습니다.
• B AND B'는 항상 0이므로, 최종 표현식은 A입니다.

1. 풀이 5:

• (A ⊕ B) ⊕ B는 결합 법칙에 의해 A ⊕ (B ⊕ B)로 변환됩니다.
• B ⊕ B는 항상 0이므로, 최종 표현식은 A입니다.