아날로그와 디지털 표현 방법
아날로그 표현
연속적으로 변화하면서 비례하는 표현
ex) 자동차의 속도, 목욕탕의 습도
디지털 표현
자릿수(digit)라는 기호에 의해 표현
이산적(discrete) 단계로 변화
디지털 표현은 연속적으로 변화하는 양을 제한적인 정밀도의 수로 나타낸 결과이다.
디지털 시스템
단지 두 개의 상태만으로 정보를 표현
2진 디지털(binary digits), 혹은 비트(bits)
디지털 시스템에서 0과 1의 상태 표현
전기적 시스템의 기술
0 : 일반적으로 낮은 전압(0 V에 가까운)
1 : 일반적으로 높은 전압
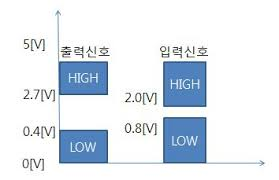
논리 레벨(Logic Levels)
LOW : 0 또는 0 V에 가까운 값
HIGH : 1, 전압의 실제 값은 시스템 기술에 따라 다름
디지털 시스템은 전압 혹은 전류의 정확한 값이 중요한 것이 아니라 이러한 값들이 갖는 범위가 중요

천이 (Transition)
디지털 신호가 한 상태에서 다른 상태로 변하는 것을 천이라고 합니다. 디지털 회로에서 천이는 주로 0(낮은 전압)과 1(높은 전압) 사이의 변화로 나타납니다.
예를 들어, 디지털 신호가 0에서 1로 변하거나 1에서 0으로 변하는 순간을 천이라고 합니다.
에지 (Edge)
에지는 천이와 유사한 개념으로, 신호가 변하는 순간을 지칭합니다. 에지는 주로 두 가지 형태로 나뉩니다: 상승 에지와 하강 에지.
에지는 신호가 변하는 순간을 포착하여 특정 동작을 수행하는 데 사용됩니다. 예를 들어, 클럭 신호의 에지를 이용해 트리거 조건을 설정할 수 있습니다.
하강 에지 (Falling Edge)
하강 에지는 신호가 높은 상태(1)에서 낮은 상태(0)로 변하는 순간을 의미합니다.
예를 들어, 클럭 신호가 1에서 0으로 변할 때 발생하는 순간이 하강 에지입니다.
하강 에지는 트리거 신호로 사용될 수 있으며, 플립플롭과 같은 디지털 회로 요소에서 특정 동작을 유발할 수 있습니다.
상승 에지 (Rising Edge)
상승 에지는 신호가 낮은 상태(0)에서 높은 상태(1)로 변하는 순간을 의미합니다.
예를 들어, 클럭 신호가 0에서 1로 변할 때 발생하는 순간이 상승 에지입니다.
상승 에지는 역시 트리거 신호로 사용될 수 있으며, 플립플롭과 같은 디지털 회로 요소에서 특정 동작을 유발할 수 있습니다.


1, 3, 4, 8을 digit, 103, 102, 101, 100을 positional number 라고 한다.
N진법을 표현하려면 (a1a0)N 과 같은 형태로 표기하면 된다.
예를 들어 16진법 AC는 (AC)16처럼 표기한다.
10진법
0~9 10개의 숫자 혹은 기호로 구성되어 있다.
10진수의 위치 값은 10의 거듭제곱으로 주어진다.
2진법
2개의 기호 또는 0과 1의 수치를 사용한다
2진수의 위치 값은 2의 거듭제곱으로 주어진다.
N 비트의 최대 계수 가능 수는 2N이다.
10진수 환산 시 최대 표현 가능 범위는 2N−1이다.
8진법 (Octal)
8진법은 0부터 7까지의 숫자를 사용합니다.
16진법 (Hexadecimal)
16진법은 0부터 9까지의 숫자와 A, B, C, D, E, F를 사용합니다. 여기서 A는 10, B는 11, C는 12, D는 13, E는 14, F는 15를 나타냅니다.
10진법에서 다른 진법으로 변환
10진수 255를 2진수, 8진수, 16진수로 변환하기
2진법으로 변환 (Binary)
- 255를 2로 나눔
- 255 ÷ 2 = 127, 나머지 1
- 127 ÷ 2 = 63, 나머지 1
- 63 ÷ 2 = 31, 나머지 1
- 31 ÷ 2 = 15, 나머지 1
- 15 ÷ 2 = 7, 나머지 1
- 7 ÷ 2 = 3, 나머지 1
- 3 ÷ 2 = 1, 나머지 1
- 1 ÷ 2 = 0, 나머지 1
- 나머지를 역순으로 읽으면 11111111이 됩니다.
- 2진수: 11111111
8진법으로 변환 (Octal)
- 255를 8로 나눔
- 255 ÷ 8 = 31, 나머지 7
- 31 ÷ 8 = 3, 나머지 7
- 3 ÷ 8 = 0, 나머지 3
- 나머지를 역순으로 읽으면 377이 됩니다.
- 8진수: 377
16진법으로 변환 (Hexadecimal)
- 255를 16으로 나눔
- 255 ÷ 16 = 15, 나머지 15 (F)
- 15 ÷ 16 = 0, 나머지 15 (F)
- 나머지를 역순으로 읽으면 FF가 됩니다.
- 16진수: FF
다른 진법에서 10진법으로 변환
2진수 1101을 10진수로 변환하기
각 자리의 숫자에 2의 자릿수 제곱을 곱함
1×23+1×22+0×21+1×20
= 1×8+1×4+0×2+1×1
= 8+4+0+1 = 13
- 10진수: 13
8진수 17을 10진수로 변환하기
각 자리의 숫자에 8의 자릿수 제곱을 곱함
1×81+7×80
= 1×8+7×1
= 8+7 = 15
- 10진수: 15
16진수 1A를 10진수로 변환하기
- 각 자리의 숫자에 16의 자릿수 제곱을 곱함
1×161+A×160
= 1×16+10×1 ※ A는 10을 의미
= 16+10 = 26
- 10진수: 26
2진법, 8진법, 16진법 간의 변환
2진수 11011011을 8진수로 변환하기
2진수를 3자리씩 묶음 (오른쪽부터)
110 110 11 → 011 011 011 (앞에 0을 추가해서 3자리로 만듦)
각 묶음을 8진수로 변환:
011 → 3
011 → 3
011 → 3
8진수: 333
2진수 11011011을 16진수로 변환하기
2진수를 4자리씩 묶음 (오른쪽부터):
1101 1011
각 묶음을 16진수로 변환:
1101 → D
1011 → B
16진수: DB
복습 문제
2진수 변환
- 10진수 42를 2진수, 8진수, 16진수로 변환하기
- 10진수 100을 2진수, 8진수, 16진수로 변환하기
- 10진수 75를 2진수, 8진수, 16진수로 변환하기
- 10진수 200을 2진수, 8진수, 16진수로 변환하기
- 10진수 150를 2진수, 8진수, 16진수로 변환하기
- 10진수 85를 2진수, 8진수, 16진수로 변환하기
- 10진수 33를 2진수, 8진수, 16진수로 변환하기
- 10진수 255를 2진수, 8진수, 16진수로 변환하기
- 10진수 64를 2진수, 8진수, 16진수로 변환하기
- 10진수 120을 2진수, 8진수, 16진수로 변환하기
- 정답1
- 2진수: 101010
- 8진수: 52
- 16진수: 2A
- 정답2
- 2진수: 1100100
- 8진수: 144
- 16진수: 64
- 정답3
- 2진수: 1001011
- 8진수: 113
- 16진수: 4B
- 정답4
- 2진수: 11001000
- 8진수: 310
- 16진수: C8
- 정답5
- 2진수: 10010110
- 8진수: 226
- 16진수: 96
- 정답6
- 2진수: 1010101
- 8진수: 125
- 16진수: 55
- 정답7
- 2진수: 100001
- 8진수: 41
- 16진수: 21
- 정답8
- 2진수: 11111111
- 8진수: 377
- 16진수: FF
- 정답9
- 2진수: 1000000
- 8진수: 100
- 16진수: 40
- 정답10
- 2진수: 1111000
- 8진수: 170
- 16진수: 78
16진수 변환 문제
- 16진수 3F를 2진수, 8진수, 10진수로 변환하기
- 16진수 A7을 2진수, 8진수, 10진수로 변환하기
- 16진수 1C를 2진수, 8진수, 10진수로 변환하기
- 16진수 B4를 2진수, 8진수, 10진수로 변환하기
- 16진수 8E를 2진수, 8진수, 10진수로 변환하기
- 16진수 7B를 2진수, 8진수, 10진수로 변환하기
- 16진수 4D를 2진수, 8진수, 10진수로 변환하기
- 16진수 9A를 2진수, 8진수, 10진수로 변환하기
- 16진수 2F를 2진수, 8진수, 10진수로 변환하기
- 16진수 E3를 2진수, 8진수, 10진수로 변환하기
- 정답
- 2진수: 111111, 8진수: 77, 10진수: 63
- 2진수: 10100111, 8진수: 247, 10진수: 167
- 2진수: 11100, 8진수: 34, 10진수: 28
- 2진수: 10110100, 8진수: 264, 10진수: 180
- 2진수: 10001110, 8진수: 216, 10진수: 142
- 2진수: 1111011, 8진수: 173, 10진수: 123
- 2진수: 1001101, 8진수: 115, 10진수: 77
- 2진수: 10011010, 8진수: 232, 10진수: 154
- 2진수: 101111, 8진수: 57, 10진수: 47
- 2진수: 11100011, 8진수: 343, 10진수: 227
'전기 · 전자 · 회로 > 디지털 공학' 카테고리의 다른 글
| 디지털 공학 6화 - 조합 논리 회로 분석 및 구현 예제 (1) | 2024.08.07 |
|---|---|
| 디지털 공학 5화 - 주관식/객관식 문제 해설 (0) | 2024.08.07 |
| 디지털 공학 4화 - 대안 표시, EN/DISABLE, TTL, 간단한 실습 (0) | 2024.08.07 |
| 디지털 공학 3화 - 논리 회로 특성, 코드 (0) | 2024.08.06 |
| 디지털 공학 2화 - 펄스, 논리 연산, 게이트 (0) | 2024.08.06 |