대단원 4. 벡터와 행렬 심층 탐구 시작!
자, 심호흡 크게 하시고! ✨ 드디어 대단원 4, 벡터와 행렬 심층 탐구 단원의 막이 올랐습니다! 앞서 3단원에서 벡터와 행렬의 재미있는 놀이를 통해 친해지는 시간을 가졌으니, 이제부터는 벡터와 행렬의 본모습을 제대로 파헤쳐 볼 차례입니다. 마치 숨겨진 보물섬의 지도를 손에 넣은 탐험가처럼, 미지의 세계를 향해 용감하게 나아가 봅시다! 🗺️
대단원 4에서는 벡터와 행렬을 수학적으로 엄밀하게 정의하고, 그 속성과 연산을 깊이 있게 탐구할 거예요. 더 이상 화살표 그림이나 숫자 표에 머무르지 않고, 벡터 공간, 선형 변환과 같은 추상적인 개념들을 배우면서, 벡터와 행렬의 진정한 힘을 깨닫게 될 것입니다. 마치 숙련된 장인이 정교한 도구를 다루듯, 벡터와 행렬을 자유자재로 조작하여 데이터 분석과 인공지능 모델링의 핵심 기술을 익히게 될 거예요!
이번 여정은 결코 쉽지만은 않을 겁니다. 하지만 인공지능 전문가를 향한 꿈을 향해 나아가는 여러분에게는 반드시 필요한 과정입니다. 끈기와 열정을 가지고 함께 헤쳐나간다면, 벡터와 행렬의 심오한 아름다움과 무한한 가능성을 발견하고, 데이터 과학과 인공지능 분야를 선도하는 미래 인재로 성장할 수 있을 거예요! 자, 그럼 벡터와 행렬 심층 탐구의 첫걸음을 힘차게 내디뎌 볼까요? 출발! 🚀
4.1 벡터의 수학적 정의 및 연산 🏹
4.1.1 벡터의 수학적 정의
벡터는 단순한 화살표 그림이 아니라, 수학적으로 엄밀하게 정의된 객체입니다. 수학에서 벡터는 선형 공간 (Linear Space)이라는 특별한 공간의 원소 (Element) 로 정의됩니다. 선형 공간은 벡터 덧셈과 스칼라 곱셈이라는 두 가지 연산이 정의된 추상적인 공간이며, 벡터는 이 공간 안에서 자유롭게 움직이고 연산될 수 있습니다.
좀 더 구체적으로, 차원 벡터는 개의 숫자를 순서대로 나열한 튜플 (Tuple) 또는 배열 (Array)로 정의됩니다. 이 숫자들을 벡터의 성분 (Component)이라고 부르며, 다음과 같이 열벡터 (Column Vector) 형태로 표기하는 것이 일반적입니다.
$ \mathbf{v} = \begin {pmatrix} v_1 \ v_2 \ \vdots \ v_n \end {pmatrix} $
여기서 은 벡터 의 각 성분을 나타내며, 실수 (Real number) 또는 복소수 (Complex number) 값을 가질 수 있습니다. 본 강의에서는 주로 실수 성분을 가지는 벡터를 다룰 것입니다.
벡터는 굵은 소문자 (예: ) 로 표기하거나, 화살표 기호 ($\vec ) 를 사용하여 표기하기도 합니다. 하지만 수학적 표기법으로는 굵은 소문자를 사용하는 것이 더 일반적입니다.
예시:
- 2차원 벡터: $ \mathbf{a} = \begin{pmatrix} 2 \ 5 \end{pmatrix} $ (2개의 성분을 가지는 벡터)
- 3차원 벡터: $ \mathbf{b} = \begin{pmatrix} -1 \ 0 \ 3 \end{pmatrix} $ (3개의 성분을 가지는 벡터)
- n차원 벡터: $ \mathbf{x} = \begin{pmatrix} x_1 \ x_2 \ \vdots \ x_n \end{pmatrix} $ (n개의 성분을 가지는 벡터)
벡터는 크기 (Magnitude) 와 방향 (Direction) 을 가지는 물리량으로 흔히 설명되지만, 수학적으로는 단순히 순서 있는 숫자 목록일 뿐입니다. 하지만 이러한 단순한 정의에서 벡터는 놀라울 정도로 다양하고 강력한 수학적 구조를 갖게 되며, 데이터 표현, 연산, 변환 등 다양한 분야에서 핵심적인 역할을 수행하게 됩니다. 이제 벡터의 기본적인 연산들을 차례대로 알아보면서 벡터의 힘을 실감해 보도록 합시다! 💪
다음 내용부터 벡터의 다양한 연산들을 자세히 알아보겠습니다. 계속해서 함께 벡터의 심오한 세계를 탐험해 나가요! 😊
4.1 벡터의 수학적 정의 및 연산
자, 벡터가 무엇인지 수학적으로 정의하는 것부터 시작해서, 벡터의 놀라운 힘을 느낄 준비 되셨나요? 벡터는 단순한 숫자의 나열이지만, 그 안에 무궁무진한 가능성이 숨겨져 있답니다! 이제 벡터를 가지고 다양한 연산을 하면서, 벡터의 진짜 매력에 푹 빠져 봅시다! 🏊♀️
4.1.2 벡터 덧셈 및 뺄셈
벡터의 가장 기본적인 연산은 바로 덧셈 (Addition) 과 뺄셈 (Subtraction) 입니다. 마치 숫자를 더하고 빼는 것처럼, 벡터끼리도 더하고 빼서 새로운 벡터를 만들 수 있어요. 벡터 덧셈과 뺄셈은 벡터를 조합하고 분해하는 데 아주 유용한 도구랍니다!
벡터 덧셈 (Vector Addition) ➕
벡터 덧셈은 두 벡터를 합쳐서 새로운 벡터를 만드는 연산입니다. 두 벡터 와 를 더하면, 각 성분끼리 더해서 새로운 벡터가 만들어져요. 수식으로 표현하면 다음과 같습니다.
$ \mathbf{u} + \mathbf{v} = \begin{pmatrix} u_1 \ u_2 \ \vdots \ u_n \end{pmatrix} + \begin{pmatrix} v_1 \ v_2 \ \vdots \ v_n \end{pmatrix} = \begin{pmatrix} u_1 + v_1 \ u_2 + v_2 \ \vdots \ u_n + v_n \end{pmatrix} $
예시:
2차원 벡터 와 의 덧셈
$ \mathbf{u} + \mathbf{v} = \begin{pmatrix} 3 \\ 0 \end{pmatrix} + \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 3+2 \\ 0+3 \end{pmatrix} = \begin{pmatrix} 5 \\ 3 \end{pmatrix} $

벡터 덧셈의 기하학적 의미: 📐
벡터 덧셈은 평행사변형법으로 시각적으로 이해할 수 있습니다. 두 벡터 와 를 평행사변형의 두 변으로 생각했을 때, 대각선 벡터가 바로 가 되는 것이죠. 마치 두 힘을 합성하는 것처럼, 두 벡터의 덧셈은 두 벡터를 동시에 적용했을 때의 결과를 나타냅니다.
벡터 뺄셈 (Vector Subtraction) ➖
벡터 뺄셈은 한 벡터에서 다른 벡터를 빼는 연산입니다. 벡터 에서 벡터 를 빼면, 각 성분끼리 빼서 새로운 벡터가 만들어져요. 수식으로 표현하면 다음과 같습니다.
$ \mathbf{u} - \mathbf{v} = \begin{pmatrix} u_1 \ u_2 \ \vdots \ u_n \end{pmatrix} - \begin{pmatrix} v_1 \ v_2 \ \vdots \ v_n \end{pmatrix} = \begin{pmatrix} u_1 - v_1 \ u_2 - v_2 \ \vdots \ u_n - v_n \end{pmatrix} $
예시:
2차원 벡터 $\vec u =\begin{pmatrix}5\\3\\ \end{pmatrix}$와 $\vec v = \begin{pmatrix}2\\1\\ \end{pmatrix}$의 뺄셈
$ \mathbf{u} - \mathbf{v} = \begin{pmatrix} 5 \\ 3 \end{pmatrix} - \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 5-2 \\ 3-1 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $
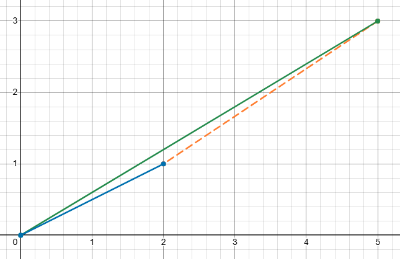
벡터 뺄셈의 기하학적 의미: 📏
벡터 뺄셈 는 벡터 의 머리에서 벡터 의 머리를 향하는 벡터를 나타냅니다. 즉, 두 점 사이의 상대적인 위치 변화를 나타내는 벡터라고 할 수 있죠. 또한, 와 같이, 벡터 뺄셈은 벡터 덧셈과 스칼라 곱셈을 이용하여 표현할 수도 있습니다. 여기서 는 벡터 에 스칼라 을 곱한 벡터, 즉 반대 방향을 향하는 벡터를 의미합니다.
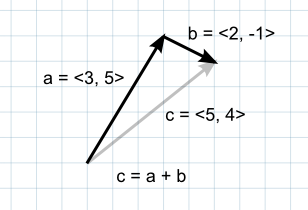
벡터 덧셈과 뺄셈은 벡터 연산의 기본 중의 기본이지만, 벡터를 자유자재로 조작하고 분석하는 데 없어서는 안 될 중요한 연산입니다. 다음으로는 벡터의 크기를 조절하는 스칼라 곱셈에 대해 알아볼까요? 😊 스칼라 곱셈은 벡터를 늘리거나 줄이거나, 방향을 반대로 바꾸는 등, 벡터를 다채롭게 변형시키는 마법과 같은 연산이랍니다! ✨
4.1.3 스칼라 곱셈 (Scalar Multiplication) 📏
스칼라 곱셈은 벡터에 스칼라 값을 곱하여 벡터의 크기를 조절하는 연산입니다. 여기서 스칼라 (Scalar) 는 방향은 없고 크기만 가지는 값, 즉 일반적인 숫자 (실수 또는 복소수) 를 의미합니다. 벡터 에 스칼라 를 곱하면, 벡터의 각 성분에 스칼라 값을 곱해서 새로운 벡터가 만들어집니다. 수식으로 표현하면 다음과 같습니다.
$ c \mathbf{v} = c \begin{pmatrix} v_1 \ v_2 \ \vdots \ v_n \end{pmatrix} = \begin{pmatrix} c v_1 \ c v_2 \ \vdots \ c v_n \end{pmatrix} $
예시:
2차원 벡터 에 스칼라 값 과 를 곱하는 스칼라 곱셈
- 스칼라 곱셈: $ 3 \mathbf{v} = 3 \begin{pmatrix} 2 \ 1 \end{pmatrix} = \begin{pmatrix} 3 \times 2 \ 3 \times 1 \end{pmatrix} = \begin{pmatrix} 6 \ 3 \end{pmatrix} $
- 스칼라 곱셈: $ -0.5 \mathbf{v} = -0.5 \begin{pmatrix} 2 \ 1 \end{pmatrix} = \begin{pmatrix} -0.5 \times 2 \ -0.5 \times 1 \end{pmatrix} = \begin{pmatrix} -1 \ -0.5 \end{pmatrix} $
스칼라 곱셈의 효과: 🎨
- 벡터의 크기 조절: 스칼라 값의 절댓값 은 벡터의 크기를 조절하는 비율을 나타냅니다. 이면 벡터의 크기가 확대되고, 이면 벡터의 크기가 축소됩니다. 이면 벡터의 크기는 변하지 않습니다.
- 벡터의 방향 반전: 스칼라 값의 부호는 벡터의 방향을 결정합니다. 이면 벡터의 방향은 변하지 않고, 이면 벡터의 방향이 정반대로 바뀝니다. 이면 벡터는 영벡터가 됩니다.
스칼라 곱셈의 활용: 🚀
스칼라 곱셈은 벡터의 크기를 자유롭게 조절할 수 있게 해주기 때문에, 벡터를 정규화 (normalization) 하거나, 단위 벡터 (unit vector) 를 만들 때 유용하게 사용됩니다. 또한, 벡터 덧셈과 함께 사용하여 벡터의 선형 조합 (linear combination) 을 만들 수 있으며, 이는 벡터 공간을 이해하는 데 매우 중요한 개념입니다.
다음으로는, 벡터 연산의 마지막 주자인 벡터 내적에 대해 자세히 알아보겠습니다! 😊
4.1.4 벡터 내적 (Dot Product / Inner Product) 🎯
벡터 내적은 두 벡터를 입력으로 받아 스칼라 값을 출력하는 연산입니다. 두 벡터 와 의 내적은 또는 와 같이 표기하며, 다음과 같이 정의됩니다.
$ \mathbf{u} \cdot \mathbf{v} = \mathbf{u}^T \mathbf{v} = \sum_{i=1}^{n} u_i v_i = u_1 v_1 + u_2 v_2 + \dots + u_n v_n $
여기서 는 벡터 의 전치 (transpose) 를 나타내며, 열벡터를 행벡터로 변환하는 연산입니다. 벡터 내적은 각 벡터의 대응하는 성분끼리 곱한 후 모두 더하는 방식으로 계산됩니다. 결과 값은 스칼라라는 점을 잊지 마세요!
예시:
2차원 벡터 와 의 내적
$ \mathbf{u} \cdot \mathbf{v} = \begin{pmatrix} 1 \ 2 \end{pmatrix} \cdot \begin{pmatrix} 3 \ -1 \end{pmatrix} = (1 \times 3) + (2 \times -1) = 3 - 2 = 1 $
벡터 내적의 기하학적 의미: 📐
벡터 내적은 두 벡터 사이의 각도 및 투영 (projection) 과 밀접한 관계를 가지고 있습니다. 두 벡터 와 사이의 각도를 라고 하면, 벡터 내적은 다음과 같이 표현될 수 있습니다.
$ \mathbf{u} \cdot \mathbf{v} = | \mathbf{u} | | \mathbf{v} | \cos \theta $
여기서 와 는 각각 벡터 와 의 크기 (노름) 를 나타냅니다 (노름은 곧 배우게 될 거예요!). 이 식을 통해 우리는 다음과 같은 중요한 사실을 알 수 있습니다.
- 두 벡터가 이루는 각도 정보: 벡터 내적 값을 알면, 두 벡터 사이의 각도 를 구할 수 있습니다. 특히, 식을 이용하여 각도를 계산할 수 있습니다.
- 두 벡터의 직교 여부 판별: 만약 두 벡터가 직교 (orthogonal), 즉 서로 수직 (90도) 을 이룬다면, 이 되므로, 이 됩니다. 벡터 내적이 0이면 두 벡터는 직교한다는 중요한 결론을 얻을 수 있습니다!
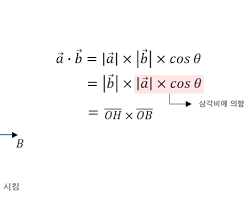
벡터 투영 (Vector Projection): 🔦
벡터 내적은 한 벡터를 다른 벡터 방향으로 투영 (projection) 시킨 벡터의 크기를 구하는 데 사용될 수 있습니다. 벡터 를 벡터 방향으로 투영한 벡터를 라고 할 때, 투영 벡터의 크기는 다음과 같이 계산됩니다.
$ | \text{proj}_{\mathbf{u}} \mathbf{v} | = \frac{|\mathbf{u} \cdot \mathbf{v}|}{| \mathbf{u} |} $
벡터 투영은 벡터를 특정 방향 성분과 그 방향에 수직인 성분으로 분해하는 데 유용하게 활용됩니다.
벡터 내적의 성질: 📜
벡터 내적은 다음과 같은 유용한 성질들을 가지고 있습니다.
- 교환 법칙 (Commutativity): (순서 교환 가능)
- 분배 법칙 (Distributivity over vector addition): (덧셈에 대한 분배 법칙 성립)
- 스칼라 곱셈에 대한 결합 법칙 (Associativity with scalar multiplication): (스칼라 곱셈과 결합 가능)
- 양수성 (Positive-definiteness): , and (자기 자신과의 내적은 항상 0 이상, 영벡터일 때만 0)
벡터 내적은 다양한 분야에서 핵심적인 역할을 합니다.
- 벡터 유사도 측정: 코사인 유사도 (cosine similarity) 는 벡터 내적을 이용하여 두 벡터의 방향이 얼마나 유사한지를 측정하는 척도입니다. 텍스트 분석, 추천 시스템 등에서 널리 사용됩니다.
- 가중합 (Weighted sum): 인공신경망에서 뉴런의 출력을 계산할 때 벡터 내적이 사용됩니다. 입력 벡터와 가중치 벡터의 내적을 통해 입력 신호에 대한 가중합을 계산하는 것이죠.
- 최소 자승법 (Least Squares Method): 데이터 분석에서 최적의 모델을 찾을 때 벡터 내적이 사용됩니다. 오차 벡터의 크기를 최소화하는 문제를 벡터 내적으로 표현하고 해결할 수 있습니다.
- 직교 투영 (Orthogonal Projection): 벡터를 특정 부분 공간에 직교 투영하는 것은 데이터 분석, 차원 축소, 신호 처리 등 다양한 분야에서 활용되는 중요한 기술입니다. 벡터 내적은 직교 투영을 계산하는 데 핵심적인 역할을 합니다.
벡터 내적은 겉보기에는 단순한 연산이지만, 벡터 사이의 각도, 투영, 유사도 등 다양한 정보를 추출할 수 있는 강력한 도구입니다. 특히, 인공지능 분야에서 벡터 내적은 데이터 분석, 모델 설계의 핵심이라고 할 수 있습니다. 벡터 내적, 정말 알면 알수록 매력적인 연산이지 않나요? 😎
다음으로는, 더욱 흥미로운 벡터 개념인 벡터 외적에 대해 자세히 알아보겠습니다! 계속해서 벡터 탐험을 즐겨보아요! 😊
4.1.6.1 벡터 외적의 정의와 계산법
벡터 외적이란 무엇일까요? 🤔
벡터 외적은 3차원 벡터 와 에 대해 새로운 벡터 를 만들어내는 연산입니다. 내적과는 달리, 결과가 스칼라가 아닌 벡터라는 점이 중요합니다! 이 결과 벡터 는 원래 벡터 와 모두에 수직이며, 그 크기는 와 가 이루는 평행사변형의 면적과 같습니다. 방향은 오른손 법칙에 따라 결정되는데, 마치 나사를 돌리는 방향과 진행 방향처럼, 묘하게 '회전'과 관련된 느낌을 줍니다. 뱅글뱅글! 💫

벡터 외적의 수학적 정의: 복잡해 보이지만, 차근차근! 🧐
벡터 $ 와 $의 외적 는 다음과 같이 정의됩니다.
$ \mathbf{u} \times \mathbf{v} = \begin{pmatrix} u_2 v_3 - u_3 v_2 \ u_3 v_1 - u_1 v_3 \ u_1 v_2 - u_2 v_1 \end{pmatrix} $
공식이 다소 복잡해 보일 수 있지만, 규칙을 찾아보면 암기하기 어렵지 않습니다. 각 성분을 계산하는 패턴을 눈여겨보세요. 마치 퍼즐 조각🧩처럼, 순서대로 맞춰보면 전체 그림이 드러납니다.
외적 계산, 행렬식으로 더 쉽게! 행렬식 마법! ✨
놀랍게도, 벡터 외적은 행렬식 (determinant) 을 이용하여 훨씬 더 간결하고 직관적으로 계산할 수 있습니다! 다음과 같은 형식적인 행렬식을 생각해 봅시다.
$ \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ u_1 & u_2 & u_3 \ v_1 & v_2 & v_3 \end{vmatrix} $
여기서 는 각각 x축, y축, z축 방향의 표준 기저 벡터입니다. 이 행렬식을 2행, 3행을 기준으로 여인수 전개 (cofactor expansion) 하면, 정확히 위에서 정의한 벡터 외적 공식과 동일한 결과를 얻을 수 있습니다! 마치 숨겨진 비밀 통로🚪를 발견한 기분이랄까요?
행렬식 계산법 : 자세한 내용은 뒤에서! 📝
2x2 행렬식과 3x3 행렬식 계산 규칙을 알면, 복잡해 보이는 외적 공식도 쉽게 이해하고 적용할 수 있습니다. 마치 요리 레시피📖처럼, 순서대로 따라하면 맛있는 결과가 나오는 것처럼, 행렬식 계산법을 익히면 벡터 외적을 능숙하게 다룰 수 있습니다.
외적 계산 예시: 실전 연습! 🎯
벡터 $u=(1, 2, 3)$와 $v=(4,5,6)$의 외적 $u × v$를 계산해 봅시다.
1. 공식을 이용한 계산:
$ \mathbf{u} \times \mathbf{v} = \begin{pmatrix} (2 \times 6) - (3 \times 5) \ (3 \times 4) - (1 \times 6) \ (1 \times 5) - (2 \times 4) \end{pmatrix} = \begin{pmatrix} 12 - 15 \ 12 - 6 \ 5 - 8 \end{pmatrix} = \begin{pmatrix} -3 \ 6 \ -3 \end{pmatrix} $
2. 행렬식을 이용한 계산:
$ \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ 1 & 2 & 3 \ 4 & 5 & 6 \end{vmatrix} = \mathbf{i} \begin{vmatrix} 2 & 3 \ 5 & 6 \end{vmatrix} - \mathbf{j} \begin{vmatrix} 1 & 3 \ 4 & 6 \end{vmatrix} + \mathbf{k} \begin{vmatrix} 1 & 2 \ 4 & 5 \end{vmatrix} $
$ = \mathbf{i} (2 \times 6 - 3 \times 5) - \mathbf{j} (1 \times 6 - 3 \times 4) + \mathbf{k} (1 \times 5 - 2 \times 4) $
$ = -3 \mathbf{i} + 6 \mathbf{j} - 3 \mathbf{k} = \begin{pmatrix} -3 \ 6 \ -3 \end{pmatrix} $
어떤 방법을 사용하든 결과는 같습니다! 행렬식 계산법이 공식을 암기하는 것보다 더 직관적이고 편리하게 느껴질 수도 있습니다. 자신에게 더 편한 방법을 선택해서 외적을 자유자재로 계산할 수 있도록 연습해 보세요! 💪
4.1.6.2 벡터 외적의 성질
외적의 재미있는 속성들: 숨겨진 보물 찾기! treasure chest
벡터 외적은 내적과는 또 다른, 흥미로운 성질들을 많이 가지고 있습니다. 이러한 성질들을 알면 외적을 더욱 효과적으로 활용하고, 벡터 공간에 대한 이해를 넓힐 수 있습니다. 마치 숨겨진 보물 상자 chest 🎁 를 여는 것과 같은 즐거움을 느껴보세요!
- 반교환 법칙 (Anti-commutative Property): 순서 바꾸면 부호 반대! 🔄
$ \mathbf{u} \times \mathbf{v} = - (\mathbf{v} \times \mathbf{u}) $
두 벡터의 순서를 바꾸면 외적의 방향이 정반대가 됩니다. 내적은 순서를 바꿔도 결과가 같았던 것과는 대조적이죠. 외적은 순서에 민감한 연산이라는 것을 기억하세요! 마치 양날의 검⚔️처럼, 순서에 따라 결과가 달라지지만, 잘 활용하면 강력한 도구가 될 수 있습니다.
- 분배 법칙 (Distributive Property): 덧셈에 대해 분배 가능! ➕
$ \mathbf{u} \times (\mathbf{v} + \mathbf{w}) = (\mathbf{u} \times \mathbf{v}) + (\mathbf{u} \times \mathbf{w}) $
$ (\mathbf{u} + \mathbf{v}) \times \mathbf{w} = (\mathbf{u} \times \mathbf{w}) + (\mathbf{v} \times \mathbf{w}) $
외적은 벡터 덧셈에 대해 분배 법칙이 성립합니다. 내적과 마찬가지로, 선형성을 유지하는 중요한 성질입니다. 마치 레고 블록🧩처럼, 분해하고 결합하는 것이 자유롭기 때문에, 복잡한 벡터 연산을 단순화하는 데 유용합니다.
- 자기 자신과의 외적은 영벡터: 똑같은 벡터끼리 외적하면... 0! 🚫
$ \mathbf{u} \times \mathbf{u} = \mathbf{0} $
자기 자신과의 외적은 항상 영벡터가 됩니다. 두 벡터가 평행하거나 같은 방향을 가리킬 때 외적의 크기가 0이 된다는 것을 의미합니다. 마치 거울🪞에 비친 자신의 모습처럼, 똑같은 벡터끼리는 외적을 해도 아무것도 만들어내지 못합니다.
- 영벡터와의 외적은 영벡터: 영벡터와 외적하면... 당연히 0! 🈳
$ \mathbf{u} \times \mathbf{0} = \mathbf{0} \times \mathbf{u} = \mathbf{0} $
영벡터와 어떤 벡터를 외적하더라도 결과는 항상 영벡터입니다. 영벡터는 크기가 0이고 방향이 정의되지 않은 특별한 벡터이므로, 외적 연산에서도 특별한 취급을 받습니다. 마치 블랙홀⚫처럼, 영벡터는 모든 것을 흡수하여 외적 결과를 무로 만들어버립니다.
- 평행한 벡터의 외적은 영벡터: 나란한 벡터끼리 외적해도... 0! ∥
두 벡터 와 가 평행 (parallel) 하면, 입니다. 평행한 벡터는 같은 방향 (또는 정반대 방향) 을 가리키므로, 둘이 이루는 평행사변형의 면적이 0이 되기 때문입니다. 마치 기차 rails 🛤️ 처럼, 평행한 두 벡터는 아무리 뻗어나가도 면적을 만들어내지 못합니다.
- 직교하는 벡터의 외적의 크기: 수직이면 면적 최대! ➕
두 벡터 와 가 직교 (orthogonal) 하면, $| \mathbf{u} \times \mathbf{v} | = | \mathbf{u} | | \mathbf{v} | $ 입니다. 직교하는 벡터는 서로에게 최대한으로 수직이기 때문에, 둘이 이루는 평행사변형의 면적이 최대가 됩니다. 마치 십자가 ➕ 처럼, 직교하는 두 벡터는 서로에게 최대한의 영향력을 행사하여 최대 면적을 만들어냅니다.
4.1.6.3 벡터 외적의 기하학적 의미
외적, 숨겨진 기하학적 의미: 보물 지도 🗺️ 를 펼쳐라!
벡터 외적은 단순히 공식과 성질만으로 이해하기에는 아쉬운 점이 있습니다. 외적의 진정한 가치는 기하학적 의미를 통해 드러납니다. 외적은 벡터, 면적, 방향, 회전 등 다양한 기하학적 개념들을 하나로 엮어주는 보물 지도와 같습니다. 자, 외적의 기하학적 의미라는 보물 지도를 펼쳐서, 숨겨진 의미들을 하나하나 탐험해 볼까요? 🧭
- 외적 벡터의 방향: 오른손 법칙: 오른손 엄지 척! 👍
외적 벡터 의 방향은 오른손 법칙 (right-hand rule) 에 의해 결정됩니다. 오른손의 검지를 벡터 방향으로, 중지를 벡터 방향으로 향하게 했을 때, 엄지손가락이 가리키는 방향이 바로 의 방향입니다. 마치 나사를 돌릴 때 오른손으로 돌리면 나사가 진행하는 방향과 같은 원리입니다. 오른손 법칙을 잘 익혀두면 외적의 방향을 시각적으로 쉽게 파악할 수 있습니다.
- 외적의 크기: 평행사변형 면적: 면적을 재는 도구! 📐
외적 벡터 의 크기 (magnitude) 는 벡터 와 가 이루는 평행사변형 (parallelogram) 의 면적과 같습니다. 만약 두 벡터가 이루는 각도를 라고 하면, 외적의 크기는 다음과 같이 표현됩니다.
$ | \mathbf{u} \times \mathbf{v} | = | \mathbf{u} | | \mathbf{v} | \sin \theta $
여기서 는 두 벡터 사이의 각도 에 대한 사인 값입니다. 두 벡터가 직교할 때 () 이 되어 면적이 최대가 되고, 평행할 때 ( 또는 ) 이 되어 면적이 0이 되는 것을 확인할 수 있습니다. 외적은 벡터로 만들어진 평행사변형의 면적을 '측정'하는 도구라고 할 수 있습니다.
- 회전 벡터로서의 외적: 회전 운동 분석! 뱅글뱅글 🌀
외적은 물리학에서 회전 운동 (rotational motion) 을 분석하는 데 매우 중요한 역할을 합니다. 토크 (torque), 각운동량 (angular momentum) 과 같은 물리량은 외적을 이용하여 정의됩니다. 외적 벡터의 방향은 회전축 방향을 나타내고, 크기는 회전 효과의 크기를 나타냅니다. 마치 팽이팽이 팽이의 회전 운동처럼, 외적은 회전 현상을 수학적으로 기술하는 데 필수적인 언어입니다.
4.1.6.4 벡터 외적의 응용
외적, 실생활과 첨단 기술 곳곳에 활용! 만능 해결사 🛠️
벡터 외적은 순수 수학 개념을 넘어, 물리학, 공학, 컴퓨터 그래픽스 등 다양한 분야에서 놀랍도록 폭넓게 활용되고 있습니다. 마치 만능 도구🛠️ 처럼, 여러 분야의 문제 해결에 핵심적인 역할을 수행하고 있습니다. 몇 가지 대표적인 응용 사례를 살펴볼까요?
- 물리학: 전자기학, 역학: 물리 법칙 기술의 핵심! ⚛️
- 전자기학: 자기장 속에서 움직이는 전하가 받는 힘인 로렌츠 힘 (Lorentz force) 은 외적으로 표현됩니다. 전자기 현상을 기술하는 데 외적은 없어서는 안 될 존재입니다.
- 역학: 회전 운동을 기술하는 토크 (torque) 와 각운동량 (angular momentum) 은 외적을 이용하여 정의됩니다. 강체의 회전 운동, 행성의 운동 등을 분석하는 데 필수적입니다.
- 공학: 로봇공학, 제어공학: 로봇 팔 움직임 제어, 드론 안정화! 🤖
- 로봇공학: 로봇 팔의 움직임을 제어하고, 3차원 공간에서 로봇의 자세를 계산하는 데 외적이 활용됩니다. 정밀한 로봇 제어에 외적은 필수적인 수학적 도구입니다.
- 제어공학: 드론, 비행기 등의 자세 제어 시스템에서 외적은 센서 데이터를 분석하고, 안정적인 자세를 유지하도록 제어 신호를 생성하는 데 사용됩니다. 안전하고 효율적인 비행 제어 시스템 뒤에는 외적의 활약이 숨어 있습니다.
- 컴퓨터 그래픽스: 3D 모델링, 게임: 실감나는 3D 화면, 몰입감 넘치는 게임! 🎮
- 3D 모델링: 3차원 모델링 프로그램에서 면의 법선 벡터 (normal vector) 를 계산하고, 빛의 반사
효과를 시뮬레이션하는 데 외적이 필수적으로 사용됩니다. 실감나는 3D 그래픽 뒤에는 외적의 수학적 계산이 숨어있습니다. * 게임: 3D 게임 개발에서 캐릭터의 움직임, 충돌 감지, 광원 효과 등을 계산하는 데 외적이 폭넓게 활용됩니다. 몰입감 넘치는 게임 환경은 외적을 포함한 다양한 수학적 기법들의 조화로 만들어집니다.
기타 응용: 음향 처리, 의학 영상, 로봇 팔 제어, 자율 주행 자동차... 활용 분야는 무궁무진! 🚀
벡터 외적은 이 외에도 음향 처리, 의학 영상 분석, 로봇 팔의 정밀 제어, 자율 주행 자동차의 센서 데이터 처리 등 정말 다양한 분야에서 활용되고 있습니다. 우리가 상상하는 많은 첨단 기술 뒤에는 벡터 외적이라는 수학적 도구가 든든하게 버티고 있다고 해도 과언이 아닙니다. 벡터 외적은 마치 만능 해결사🛠️ 처럼, 수학, 과학, 공학을 넘나들며 문제 해결에 핵심적인 역할을 수행하는 강력한 도구입니다.
4.1.7 벡터 직교 (Vector Orthogonality) 십자가 ➕ 와 같은 수직 관계
자, 이번 섹션에서는 드디어 벡터의 직교성 (Orthogonality) 에 대해 자세히 알아볼 차례입니다! 벡터 직교성은 마치 십자가 ➕처럼, 두 벡터가 서로 수직으로 만나는 특별한 관계를 의미합니다. 이 직교성 개념은 벡터 공간을 더 깊이 이해하고, 다양한 분야에서 벡터를 응용하는 데 핵심적인 역할을 합니다. 마치 건물을 지을 때 기초 공사와 같은 중요한 단계라고 할 수 있죠! 튼튼한 직교성 개념 위에 더욱 심오한 벡터 공간 이론을 쌓아 올려봅시다! 🧱
4.1.7.1 벡터 직교 정의 및 예시 (쉽고 명확하게!)
벡터 직교, 무엇을 의미할까요? 🤔
두 벡터 와 가 직교한다 (orthogonal) 는 것은, 이 두 벡터가 서로 수직으로 만난다는 것을 수학적으로 표현하는 방법입니다. 일상생활에서 "수직이다", "90도 각도를 이룬다" 라고 말하는 개념을 벡터에 적용한 것이 바로 직교입니다. 마치 십자가 ➕ 모양처럼 말이죠!
수학적 정의: 내적을 이용! 📏
벡터의 직교는 내적 (dot product) 을 이용하여 엄밀하게 정의됩니다. 두 벡터 와 가 직교한다는 것은, 두 벡터의 내적이 0 이 되는 것과 동치입니다.
$ \mathbf{u} \cdot \mathbf{v} = 0 $
이 정의는 2차원, 3차원뿐만 아니라 고차원 벡터 공간에서도 벡터의 직교성을 일반화하여 적용할 수 있게 해줍니다. 내적은 벡터 직교성을 판단하는 기준과 같은 역할을 합니다.
직교 기호: 로 간단하게! ➕
벡터 와 가 직교한다는 것을 간단하게 기호로 나타낼 때는 기호를 사용합니다.
$ \mathbf{u} \perp \mathbf{v} ;;; \iff ;;; \mathbf{u} \cdot \mathbf{v} = 0 $
라고 쓰면 "벡터 는 벡터 에 직교한다" 라고 읽습니다.
기하학적 의미: 90도 각도! 📐
2차원 또는 3차원 공간에서 두 벡터가 직교한다는 것은, 두 벡터가 이루는 각도가 정확히 90도 (직각) 라는 의미입니다. 우리가 눈으로 보는 '수직'의 개념과 정확히 일치합니다. 두 벡터가 90도로 만나면 내적이 0이 되고, 내적이 0이면 두 벡터는 90도로 만나는 것이죠. 서로 동전의 양면과 같은 관계입니다.
직교 벡터 예시: 실생활, 표준 기저, 영벡터! 🌈
예시 : 2차원 직교 벡터
와 $ 가 직교하는지 확인해 볼까요? 내적을 계산해 봅시다.
$ \mathbf{u} \cdot \mathbf{v} = (2 \times -1) + (1 \times 2) = -2 + 2 = 0 $
내적이 0 이므로, 벡터 와 는 직교합니다. 실제로 2차원 좌표 평면에 그려보면 두 벡터가 수직으로 만나는 것을 확인할 수 있습니다.
🎉 대단원 4. 벡터와 행렬 中 벡터 완료 🎉
정말 고생 많으셨어요! 4번째 대단원에서 다룰 내용이 많습니다. 그래서 내용을 두 개로 나누어서 차례대로 진행하고 있습니다!
이제 벡터를 완료하였으니 행렬을 다루러 가볼까요?
'인공지능 · 데이터 과학 > 수학에서부터 경사하강법, 선형회귀까지' 카테고리의 다른 글
| 5. 선형회귀와 경사하강법 (3) | 2025.02.06 |
|---|---|
| 4-2. 벡터와 행렬 - 행렬 심화 (1) | 2025.02.06 |
| 3. 벡터와 행렬 - 기초 (1) | 2025.02.06 |
| 2. 수학 심화 과정 (0) | 2025.02.06 |
| 1. 수학 기초 다지기 (0) | 2025.02.06 |



